――ジョーク。ビリーバーはめったに冗談を口にしない。臨死体験狂信者と超能力者とUFOアブダクティになにか共通した特徴があるとすれば、ユーモア感覚の欠如だ。(「航路」コニー・ウィリス、大森望訳)
誰に教わったことだったか忘れたが、追いかけっこをしている狐とウサギには本質的な非対称がある。つまり、狐は今日のごちそうのために走っているのに対して、ウサギは生死を賭けて走っているのである。「ビリーバー」にユーモアが欠けているとすれば(そんな気はする)、それはおそらくかれらが生死を賭けて走っているからではないか、と思う。臨死体験、超能力、UFOによる誘拐は、確かにどれも生死を賭けるべき重要な問題だ。本当だとすれば。
しかし悲しくもそうではないのであって、これは結局、何事にも必死になってはいけない、人生、大抵のことでユーモアを忘れないようにしなければならない、ということなのかもしれない。本当に大事なことを冗談に紛らせておろそかにしてはいけないが、そんな毎日でも、しばしば一歩引いて、自分の感覚、自分の信念、自分が今やっていることを客観的に見て、疑ってみる、そういう時間はあるべきだと思うのである。
などと、へんな人生訓になってしまってはいけないが、私がモットーとしていることは「いつも心に雑文を」である。あなたが何かに憤りを覚えたとする。それを声高に主張するのもいいし、思い切って皮肉っぽい文章にして相手に送りつけるのもいいだろう。しかし、そこで立ち止まり、そういう憤りを覚えた自分を見下ろしてみる。腹が立ったそのときに後ろから見てみる。少なくともそうするだけで人生が少し楽しくなるし、とりかえしのつかない間違いをしでかすことも少なくなるのではないか、と思う。
先だって、ウェブ上で新聞を読んでいて、こういうタイトルの記事に出会った。
「正解の4割は『1×』 センター試験、数学の答えに偏り」
内容はこんな感じである。ある大学教授が大学院生とともに行った研究で、十数年分のセンター試験の数学の全問題を調べてみた。センター試験の数学科目においては、二桁や三桁の数字が答えになる問題があって、たとえば計算の答えが「205」ならマークシートを三列使ってに2、0、5と三つマークする、そういう形式になっていることがある。彼らはその数字の偏りを調べてみた。そうすると、
・解答が二桁の正の数のときに、十の位が1だったのは458問中185問(40%)。
・解答が三桁の正の数のときに、百の位が1だったのは86問中45問(52%)。
であった。これは単純なランダムから予想される1割や、ベンフォードの法則から予測される約三割に比べて多い。
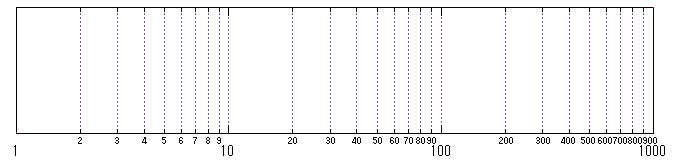
「ベンフォードの法則」というのは、今回初めて知ったのだが、ランダムな数字の最高位の桁は、1になりやすい、というものである。ここで「ランダム」というのは桁数まで含めてランダム、ということで、たとえばいろいろな国の面積などがそれにあたるのだと思う。ベンフォードの法則は、軸が対数になったグラフを見ると直感的に理解できる。対数のグラフというのは軸上に1、10、100…を等間隔に取った、

こういうものだが、確かに「1」のところが広くて他の数字がだんだん狭くなっているのがわかる。このグラフに目隠ししてダーツを投げつければ「1」や「2」「3」のエリアに命中する可能性が他より高くなるだろう。だいたいこのような意味で、一番上の桁は、他の数字よりも1(または2や3)になりやすいのである。これは、でっち上げた数字を見破るのに有効に使える。なるほど。
閑話休題、記事の研究によれば、要するにこの効果で予期されるよりもさらに高い確率で、センター試験の答えの最高位は1になりやすいということである。私はもう、読んでいてなんて面白い研究だ、と思った。こんな研究をして日々を送りたかったような気がする。ところが、読んでいくと、どうも違う。研究者のほうでは、真剣に、問題提起として、この研究をしていたような雰囲気が、そこはとなく伝わってくるのだ。少なくとも記事は、いかめしくこう結ばれている。
「センター試験に限らず、大学入試全般でマークシートによる空欄補充方式が多くなっている。芳沢さんは『採点が楽だからと安易な方式に頼らず、証明など記述式の問題で受験生の本当の力をみる努力をすべきだ』と話す」
繰り返して書くが、研究は面白い。手続きは単純明快で曖昧さはないし、統計的なばらつきによる誤差を考慮していないことが気になる程度で、1が多いという結果にも問題はなく、興味深い結果が出たと思う(それに、誤差は問題の細部だから新聞記事から省かれているだけかもしれない)。しかしこれをもってセンター試験全体を批判するのはどうか。言っていることは正論かもしれないが、この研究からまっすぐ導かれる結論とはちょっと違う。1が多いから「もっと答えをランダムに」であり「マークシートはとにかくダメだ」ではないはずなのだ。
そこが残念だと思う。これを使って、私ならもっと面白い文章が書けたのに、と感じるのは傲慢ではないと思いたい。問題がわからなくても一桁目を1にしておけば正答率が上がる、こんな試験不公平だよね、ではなくて、そういう癖が全体として見えてくる、そのことに知的な興味を抱きたいのだ。他人を責めるのではなく、面白がりたい。そして、こんな研究そもそも無意味かもね、という自省を、どこかに込めたい。
記事の中にも、それらしいところ、研究者が気づきかけていると思える箇所が、実はある。嘘かマコトか、出題者がセンター試験の問題を作る際に「あてずっぽうでは正答が出ないように、数字を1けたから2けたにするなどの工夫をしている」とあるのだ。「それが裏目に出た」と言っている。
違うのだ。裏目に出てなんかいないのである。問題を作るほうが究極的に愚かで、こうして一桁から無理やり二桁にしているとしよう。それでもって、二桁になった答えの一桁目はもう全部1、1に決まっているとしよう。ところが、それでもあてずっぽうで得点を得る確率は変わらないのだ。0から9の十個の数字から答えを当てるゲームが、10から19の間のどれかを当てるゲームになるだけのことだから。無理に二桁にした出題は、その効果は不十分だとしても、少なくとも逆効果ではないのだ。
そして実際には、一桁目は1と決まっているわけではない。六割は他の数字である。10から99のうち一つを当てる確率は90分の1、1.1%だが「四割は一桁目が1」というデータを使って十の位を常に1にマークしたところで、当たる確率は4%にしかならない。四倍になると見るか、3%増えただけ、と見るかで違うだろうが、そう、それだけのことなのだ。
ここでおかしい、と気づくべきだったと思う。おかしいから、考え方なり記事の書きかたを直すべきだ、ではない。おかしいから、自分のやっていることに生死なんかかかっていないことに気が付いて、笑えればよかったのだ。大した問題ではないんですが、問題の作り方はもう少し考えたほうがいいよね、と発表すればいい。これで雑文の一本も書いて、自分のホームページにでも載っけておいたらそれでいいのだ。
想像してみる。記事では試験制度を、特に数学のそれを憎んでいる記者のせいで、こうなってしまったけれども、本当は研究者サイドでは私なんかが思うようなことは何もかも気がついていているのではないか。研究を始めた手前、数学に弱い記者を騙しておいて、適当に誰も反論できない正論を述べてお茶を濁しただけだと。本当に、そうであればいいと思う。自分を笑えないのは、いいことじゃないと思うのだ。
そうとも、だから雑文を書こう。