後悔というものは生きているだけで積み重なってゆくもので、あるとき誰かに何かを言われ、いったんは引き下がったものの、すぐその理不尽さに気づき、いつまでも納得できない、などということは私も多い。「席をゆずれ」と言われて、はいと譲ったのだが、よく考えたらそんな義理はないんじゃないか、というようなことである。「そんな義理ないですよね?」と言えなかった悔しさがまずあるわけだが、このときに使えばよかったうまい言い回し、席を譲らないで済むし誰でも納得できるすっきりした論理、一見まったく違うことなのに深いところで類似していて説明に使える別の事例、といったものは、相手と意見が対立したそのとき、タイミングよく訪れるものではない。おおむね時機を逸したずうっと後、何年もなんねんも経ってから、たとえば朝、まだ起きる時間じゃないのに目が覚めてしまって、わあこれは幸せだあと三十分も寝られる、とゴロゴロしているときなどに突然訪れるのだった。
思いついてどうするか。ああそうか、なるほどそうか、こう言えばよかったのだ、ひゃっほう、これなら相手はグウの音も出ない。すごいぞ私、これで勝った、完全勝利、と思ってがばっと起き上がっても、だからもう遅いのであって、席はゆずった後なのであって、勝負で言えばずっと前に負けていてこれからも負けっぱなしなのであって、のみならずこれからは「うまく言えなかった悔しさ」にくわえ「思いついた『うまい言い方』を誰にも言えない悔しさ」もずっと抱えて生きてゆかなければならない。これは人生におけるたいへんな損失である。損失であるし、そうやって早起きしてしまうとあとで眠いのでさらに損である。そういうのを雑文とかツイッターとかに書けなかった時代の人々はどうやって生きていたのか。へそを噛んで我慢していたのか。
ということで、こういう悔しさがあるので、つまり人は学校教育には文句をつけたがるものなのだ、と思う。日本人の成績がどうという話になると教育制度を責める。いじめ問題になると学校の対応を責める。算数や国語の教え方がこうおかしいというと子供の担任の先生を責める。これは、もっともな指摘も多いのだと思うけれども「むかし、先生や友達と対立して引き下がった」「しかし後からうまいこと言う言い方を思いついた」「ところがもう遅かった」という二重三重の後悔をみんなが持っているからではないか。人間、生きているだけで後悔は積み重なってゆくので、それは学校だけに限ったことではないのだろうが、なにしろ学校にはだいたいみんな行っている。「学校に行った人」はたとえば「神姫バスに乗った人」よりもうんと多く、だからして「教育に不満のある人」は「神姫バスの停留所にある時刻表に不満がある人」よりもずっと多いわけで、そういうわけで「かけ算の順序」等に何かひとこと言いたい人がこんなに多いのだと思う。
これはもうどうしようもないので、だから先生方もそのあたりはわかっていてかなり割り引いて考えて下さっているのだと思うが、そういう話題の一つだと思う。「円周率を3で計算する」という話が、一時期ずいぶん問題になった。小学校では円を含んだ面積や円周の長さを計算する問題があるが、ここでおおむね、円周率を3.14で近似して計算することが多い。しかしこれが無駄に桁数が多く計算がたいへんであったりして、円周率を3で近似して計算させることもあってよいのではないか、そうしよう、ということに関する異論反論である。
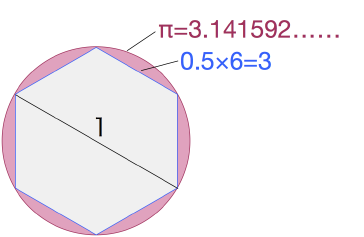
もともと円周率というものは3でもなければ3.14でもないので、これは畢竟「今の目的に十分な精度」としてどこまでの近似値を用いるかという実用上の問題なのだが、近似値に3を用いることに対する反響の中に「3を用いて計算することは、円を六角形とみなすのと同じである」というのがあって、これは面白い、と思った。円周率というのは、円の周の長さをその直径で割ったものである。ところでこの円に内接する正六角形を考えると、この辺の長さの合計はちょうど3となる。こんな感じである。

六角形で円を近似するのは、なるほどかなり雑な感じがする。上の図で見ても円と六角形の間にかなりの隙間があって、こんな栓をしたら中からだらだらケチャップやマヨネーズが漏れてきそうだ。漏れそうなのだが、いやだから、面積の話ではなくて周の長さの話なので注意が必要だが、しかし、まあこれも程度の問題である。二千年後の気候とか、銀河系にある文明の数とか、宇宙にある陽子の個数がどうとか、そういう話になると「πは1で近似する」などとやってしまっても事実上問題ない場合もある。他に不確定な要素がなんぼでもあるので、円周率だけ一生懸命桁数を上げてもなんにもならないからである。ピザやデコレーションケーキや公園の池が相手なら、六角形で十分な場合もあろう。
その「目的に応じて使用する数字の精度を決める」というのが、これで一つの難しい課題であって、小学生あたりではなかなかできないのだが、ここでふと思いつく問題として「では3.14は多角形で言うとなんなのか、近似値として3.14を使うということは、円を何角形で近似していることになるのか」がある。上記の「六角形」の議論をそのまま使うと、これは要するに「直径1の円に内接する正多角形の辺の長さの合計が3.14になるのは、何角形のときか」という問題だが、ちょっと考えてみると、一般の場合、正n角形の1辺の長さはr×sin(θ/2)×2になる。θは360度÷nだし、rは0.5なので、結局辺の長さの合計はn×sin(π/n)ということになる。
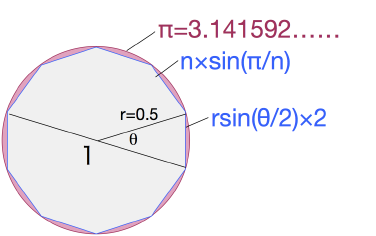
むつかしいような気がするが、グーグルの検索窓のところに「6×sin(π/6)」と入力するとちゃんと3と出る。実によい時代になったものである。だいたいどんな質問にも「ググれ」で間に合う。
あとはこれを使えば電卓仕事で結果が出るが、3.14という近似値に相当するのは、だいたいnが57のときであることがわかる。3.14という近似値を使うのは、円を正五七角形で近似することに相当する。これは内接正多角形の辺の長さに限った話なので、外接正多角形の辺の長さや、それぞれの面積から円周率(の近似値)を求めようとする場合には、また話が少しずつ違ってくる。どちらにしても上の図の焼き直しだし、関数電卓かグーグルが使えればたいした計算ではないので、いろいろやってみると面白いかもしれない。
しかし、考えてみるに、この「円周率の近似値としてふさわしいのは3か、3.14か」という議論は、円周率が3.1415……という数字の並びに大本の原因があるのではないか。というのは以前にも書いた(七進法万歳のこと)が、小数点以下2位目の「4」という数字がいかにもでっかくて切り捨てづらいというところに大きな問題があるような気がする。上のリンク先の話では、十進法でない、他の体系を使えば、うまい桁でうまく精度のよい近似値が得られてお得なのではないか(そしてそれは七進法だ)という話なのだが、それからこちら、ちっとも七進法は使われていないので、何か根本的な不都合が七進法にはあるのかもしれない。
というのは冗談だが、しかし、最近ひらめいたのだが、これは「十進法が悪い」ということもできるが、πの定義もよくないのではないか。ふつう、円周率は円の直径と周の長さの比として定義されるが、何もこれが直径との比である必要はない。たとえば円周率として定義される数字が、円の半径と周の長さの比、今の2πであったらどうだったか。ρ=2πとすると、また、rが半径とすると、
円の周の長さ(2πr)→ ρr
円の面積(πr2)→ ρr2/2
球の体積(4/3×πr3)→ 2/3ρr3
球の表面積(4πr2)→2ρr2
等となるだけで、それほど不都合があるようには見えない。考えてみると、プランク定数のhを2πで割ったものをわざわざ「hバー(hの縦棒に短い横棒がついたやつ)」というが、これもh/ρであってたいへんぐあいがよい(ような気がする)。で、それよりもよいことは、
ρ=6.283185……
なので、小学校の先生もこれを「6.3で計算しなさい」と言って何か問題があるようには思えないところである。2桁ならそんなに計算も面倒ではないし、πを3.15で近似することになるので、2桁にしてはなかなかよい近似である。πよりも大きいので内接正多角形ではないが、これは外接正三五角形の辺の長さの合計にだいたい等しい。
ということを、私はどうして「七進法万歳」を書いたときに気づかなかったのか。まったく謎なのだが、こうやって雑文として書いて「あのとき思いつかなかった悔しさ」をある程度はらすことができる。インターネットは私の精神とへその健康にたいへん役立つものであると、そう感心しているところである。