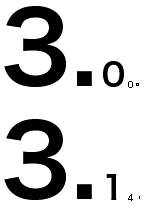
こんなのである。「こんなの」と言われても、画像が出ない環境で見ている方にはまったくわからないと思うが、要するに「3」の十分の一の面積で「1」を書き、その十分の一の面積で「4」を書き、としてあるわけだ。これを見ると、3の次に、かなり重要度において大きく引き離されて次の桁の1なり0なりがやってきて、もうその次となると、かなりどうでもいい感じであることがわかる。このような性質が、もとの算用数字からはわかりにくいではないか、ということである。
アップル恐るべし。
いや、まったくもってオカルティックかつ逆恨みックで申し訳ないのだが、アップルの悪口を書いたらとたんに手元のアイポッドシャッフルが故障して、朝夕の通勤時の楽しみがなくなると同時に書きかけの雑文のデータが全部消えてしまった。天網恢々粗にして漏らさず。悪口を書くと悪口が返ってくるのだ。私は確か昔保育園でそう習ったのではないか。
音楽はともかくとして、雑文とはなにか。雑文とアイポッドと何の関係があるのか。知らない人には説明するが、つまり、アイポッドシャッフルには「音楽を鳴らす」という機能のほか、内蔵メモリの一部を単なる USBフラッシュメモリとして使用する機能があって、私はそこに雑文一式を入れて持ち運んでいたのである。よく考えてみると、ノートパソコンのハードディスクではなくアイポッドシャッフルにしか最新の雑文がない状態というのは明らかに変だが、私の立回先何か所かで作業をしていると、いろんなバージョンが存在したり、「あの書きかけの続きが書きたいがそのデータは今手元にない」という状態になりやすい。そんなとき、最新のものはすべてリムーバブルメディアにある状態というのはひどく具合がよいのである。
ところがちっとも具合がよくなどなかった。つまり消えたのであり、なんとなくこれは壊れない、なにしろ洗濯しても壊れなかったという噂だ、などと安心していたのがよくなかった。ほぼ発表するばかりになっていた雑文が二つと、なかなか有望だった気がするアイデアが十個ほど、もろともに私の手から消えてしまったのである。アイポッドシャッフルというのは小型軽量化のためにいろんなこと(たとえば防弾性能)を無視したつくりになっているので、たぶん修理してもデータは取り戻せない。アップル恐るべしであるが、いや、嘆いていても始まらない。今日も更新できないと酒を飲んで寝てばかりでは進歩もないので、ここはがんばって思い出して書いてみることにするのである。
まず、ええと、算用数字は偉い。こんな書き出しではなかった気がするが、なんかそういう話だった。算用数字が偉いのは、数字ではなくてその数字を使った数の筆記法だと思うので「数字が偉い」と言ってしまってはいけないと思うのだが、要するにゼロがある算用数字は偉いのだ。何が偉いと言って、空位のゼロの発明によって「今の数が十個あつまるとどうなるの?」という質問から解放されるところが偉い。何を言っているのかというと、
「一万の一万倍は一億」
「その一万倍は?」
「一兆」
「その一万倍は?」
「一京」
「へえ、物知り。その一万倍は?」
「さあ」
という状態から解放されるのである。そうそう、そんな話だった。京の次の数詞がなんだったかシャッフルもろとも忘れてしまってこれ以上議論を深化できないが、ええと、算用数字ならこうだ。
「10000の10000倍は100000000」
「その10000倍は?」
「1000000000000」
「その10000倍は?」
「10000000000000000」
「へえ、物知り。その10000倍は?」
「100000000000000000000」
いくらでも続けられる。行くところまで行ったところでたとえば「無量大数の一万倍は?」でお手上げになってしまう方法より、なんぼか偉い気がするではないか。
ただ、一ついけないことは、上で既に示されているように、この無限性はわかりやすさと二律背反であるということである。たとえば、10000000000000000と100000000000000000の違いというのは、正直よくわからないわけだが、実は後者のほうがゼロが一個多い。ゼロが一個多いだけなのだが、これが実は十倍の価値の違いを意味するので、それはちょっと困るという場合、ゼロをちまちま数えるしかない。これが「一京」と「十京」なら、ちゃんと後者のほうが偉いことがわかる。なんだか説得力があるようなないような感じで、このへん、前回はもっとちゃんと書いていた気がするのだが、そこで悩んでいてはいつまでたっても書き終わらないので、次に進む。
ええと、だからそれだけではない。たとえば、
3
と、
3.141592653
の違いはどうか。いや、この下りに政治的な意味などないのでそのへんは私を信頼していただきたいが、ぱっと見た目、この二つの違いは大きい、気がする。なにしろ単なる3と、3のあとにいっぱい数字がある数字である。後者のほうがうんと偉い気がするのである。
ところがそうではあるまい。前者の数字は、別の書き方では、
3.000000000
ということになるが、これと、
3.141592653
の差、つまり、
0.141592653
は、最初の3の十分の一程度にすぎない。算用数字においては、桁を一つ右に移動するとその数字の絶対値に対する重要性は十分の一になるのだが、そのへんがぱっと見た目わかりにくいではないか、と言いたいのである。
これを払拭するには、たとえば「右に行くほど数字が小さくなる」というふうにして、書いてみるとよいのではないか。そうそう、それが言いたかったのである。つまり、
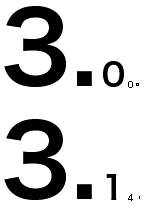
こんなのである。「こんなの」と言われても、画像が出ない環境で見ている方にはまったくわからないと思うが、要するに「3」の十分の一の面積で「1」を書き、その十分の一の面積で「4」を書き、としてあるわけだ。これを見ると、3の次に、かなり重要度において大きく引き離されて次の桁の1なり0なりがやってきて、もうその次となると、かなりどうでもいい感じであることがわかる。このような性質が、もとの算用数字からはわかりにくいではないか、ということである。
その点、漢数字やローマ数字は大小がはっきりしていて、イメージがしっかりできている気がする。ローマ数字はご存知の通り、「1」「5」「10」「50」「100」「500」「1000」というような数字にそれぞれ特定の文字が与えられていて、それを組み合わせて大きな数字を表すというものだが、これは現在の通貨単位に似ている。一円玉が一山どっさりあっても輝ける一万円札一枚にはぜんぜんかなわないということを、我々はちゃんとわかっているではないか。
ところが、それを算用数字にしたとたんによくわからなくなるのであって、通帳やカードの明細を見たときに残りの数字が1000000であれ100000であれ、どちらでもいいような気がしてくる。まことに算用数字の罠というものであり、通帳においては原則を曲げて上の桁ほど大きな文字で書いてくれれば、カード破産のような悲劇ももう少し避けられるのではないか、と言いたいのである。このへん、消えてしまったほうの文章でどう書いていたのかよく覚えていないし、特にオチがどうしても思い出せないが、ええと。
ああそうだ。それでもって実は新しいアイポッドシャッフルを性懲りもなく買ったわけで、それは通販で買ったのでカード番号を入れるだけでポンと買えて、これが現実のお金を動かす買い方をすれば、もう少しアップルに対して憎しみがわいてくるのではないか。ないか、と言いかけたところで、これ以上アップルの悪口を書いて今使っているノートパソコンが壊れたらたいへんなことになるので、ここで口をつぐむことにするのである。ああよかった。なんとなくまとまった。ええその、おっしゃることはごもっともです。次回はもうちょっとががんばります。