乱暴に総括すれば、小学生の子供を一人育てるということは、もう一度小学生として生きるということである。小学生として入学し、徐々に友達と親しくなり、集団生活について勉強してゆき、漢字を習い、時計が読めるようになり、休み時間に外で遊び、給食を残して、体育でかっこいいところを見せたり見せなかったりする。植物を育て社会見学をして生き物を育てる。プールで泳ぎ水彩画を描いてリコーダーを吹く。こういうのはすべて、ふつうに社会人として生きているうちに、いつのまにか忘れていたことで、いちいちおもしろい。
ところが、子供が勉強しているのを横から見ていると、自分がわりと、小学生をちゃんとやっていなかったことに気づいて驚くことが多い。だいたい、漢字の書き順がいいかげんである。社会や理科のさまざまな知識に関してもあやふやで、「資料を読み解け」ならなんとかなっても、覚えていることを書けという問題になると、ハタと書けないことがあったりする。忘れたのか。いや、忘れたのではない。忘れたのではないのだ。「忘れた」というのはつまり「一回は覚えていた」のであり、それは「小学生のときはちゃんやってた」ということである。そうではなくてつまり、そんな書き順など、小学生のむかしから大人になる今まで、一度も覚えたことなどなかったのである。
覚えたことがなくて、どうしたのか。ごまかした。騙し取り、かすめとり、勝ち取った(テストの点を)。先生が作った小テストみたいなものをごまかし、点数が悪い子だけやらされる再テストもまたごまかして、クラスの後ろの壁に貼ってある「漢字テストラリー」みたいなのでは、友達より明らかにシールの枚数が少ないのにそのままその学年を終えた。その後、入試やらなにやらでその手の問題が出ることもあったかもしれないが、それは問題ごと捨てた。なかったことにして先に進んだ。そうやって大人になって、どうなったかというと、小学生の問題を見て驚いているわけである。つまり、どうにかなる。やらないでも、どうにかなる勉強は、あるのだ。
いまたいへんなことを言った気がするが、そのへんは私の子供には黙っていていただくとして、そんな中で、算数だけは少し違う、気がする。私が子供の勉強を見ていたとして「これは間違えて覚えていた」「実は今までごまかしていたが、できないまま来ている」「最初からやった覚えがないし、実際できない」などというのが、算数だけはほとんど存在しない。できない問題が一つもない。有名な「かけ算の順序問題」だとか、「ゼロは自然数に含みますか」のような、わずかな例外はあるけれども、そういうのでもない限り、大人の私が今使っている知識と技術を使って、算数の問題はまず間違いなく、すべてちゃんと解けるのである。
これは、私が「算数だけはちゃんとやっていた」ということではない。この私に限って、算数だけにしろ、きちんとやっていたわけがないではないか。おそらく算数、あるいは数学という教科の持つ性質として、一つの知識なり技術が、その年その時に限り使って、それでできてもできなくても恨みっこなしこれで終わり、などというサッパリしたものでなく、次の年も、その次の年も、少しずつ内容を複雑にしながら繰り返し使ってゆくものだということがあるのだろう。
算数というのは、一見そうは見えない場合もあると思うのだが、積み重ねの教科のようである。たとえば、九九を忘れてもなんとかなったり、くり上がりの足し算がどうしてもできなければそっち方面は捨ててよい、などということはなく、もしもそういうことをすれば、次の年その先にはまったく進めなくなってしまう。しかたがないので、たとえば九九をごまかしていたとしても、次の年で掛け算の筆算を練習するころまでには追いついて、なんとかしたとか、そういう解決をしたに違いない。そうやってなんとかしたので、今もなんとかなる。いちおう高校あたりまでは学校の数学についてゆけたというような人であれば、これは誰でもそうなのではないだろうか。逆に、小学校の算数の範囲で何かできない技術があるとすれば、以後の数学の学習において、それどころではない大穴が空いている可能性が高い。
さて、そういうことなので、子供の算数を見ていると「わからない。さぼっていた。たいへんだ」という気持ちよりも、「この教え方は今思うとちょっと変なのではないか」「もっとやり方があるのではないか」と思うことのほうが多い。小学校の算数の教え方を見ていて、つい何かひとこと言いたくなるというのは、算数という教科の持つ実にこの性質のせいではないかと思ったりもするのだが、筆算というのはどうなのだろう、と思うことがあった。
筆算とは何か。いちから考えてみると、筆算とは、複雑な加減乗除の計算をやるうえで、通常の式とはべつのかたちに与えられた数値を配置し、数列に特定のオペレーションを加えることで答えを得る技術である。たぶん。ええっとつまり、計算するとき、そのまんまだととても答えが出ない場合、数字を紙の上に並べるわけだ。足し算ならこう、引き算ならこう、という数の並べ方がある。並べると、あとは決められた手順にしたがって、数字を操作すればよい。この操作のことを「計算」と言っていいのかどうか、たとえば2たす4を私たちは計算しているわけではなくて、頭の中の表を引っ張り出してきて「6」という答えを写して書くだけだが、これは計算か、記憶の参照ではないか、という話はあると思うのだが、まあそうやって、しっかりと定義されていて、こういうときは2だが気分によって3のときもあるみたいなあいまいさがない、決められた手続きを経て、その過程で一度も間違いなく手順をこなすことができれば、正しい答えが紙の上に現れる。筆算とは、そういうものだと思う。つまり、むつかしいことをいえばアルゴリズムである。
そういうものだとして、割り算の筆算。これは、ちょっとどうなのか。
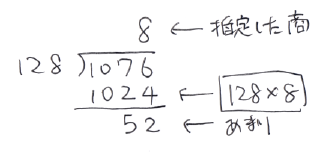
たとえば、1076÷128という問題が出たとする。これを筆算で計算するとして、小学校では次のように教えている。

何も問題ないように見える。128に何を掛けたら1076に近くなるかを推定し、8を入れてみる。128×8の答えを計算し、1024を得る。1076からこれを引けば、あまり52である。教科書にそう書いてある。
ところが、これはおかしいではありませんか、変ではないですかという、今回は実はそういうお話です。128に何を掛けたら1076に近くなるか。8ですよね? 普通8が思いつきますよね? と教科書は言う。いやしかしそんなことはあるまい。これが当たり前だとしたらあなたがちょっと2進数に慣れているせいで、128の8倍が1024であることを覚えているからである(そういう人は多いような気がしてきたけど)。2進数なんか見たことがない普通の小学生や私は、まあ7ぐらいでいいかと思ったり、いや9いけるやろ9めっちゃイケてるやろ、と思ったりするものであり、そもそも最初から商が8だとわかっていたら割り算なんてする必要はない。それで、そうやって誤って推定するとどうなるかというと、
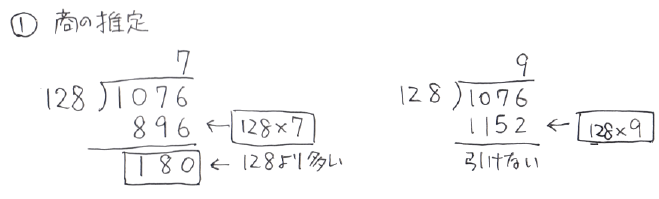
このようになる。あまりが128よりも大きかったり、あまりを求める引き算ができなくなったりして、先に進めなくなるのである。こういうときどうするか。教科書は簡単に「そういう場合は消してやりなおせ」と教えている。鉛筆を消しゴムに持ち替えて、間違っていた商と、128と7を掛けたり、9を掛けたり、それなりの手間をかけた計算結果を、消しゴムで消してやりなおしになるのである。
私は言いたい。アホウかと。何を考えているのかと。
そもそも、筆算というのはアルゴリズムであるべきだ。決められた、誰でもできる手順にしたがって操作すれば、答えにまっしぐらにたどり着けるものであってほしい。その際、紙と鉛筆以外の道具は使わないほうがいいし、「やりなおし」は、できるだけ存在しないほうがいいし、「推定」などはしないで済むに越したことはない。だいたい「商がいくらくらいか考える」というのができが悪い。128に何を掛けたら1076を超えない範囲でもっとも近くなるかを正しい見積もる、それはそれで重要な技術である気はするが、割り算のたびにこの推定が不可欠である必要はない、気がする。学校で教わる他の筆算、足し算や引き算やかけ算はまずまずよくできているのに、この割り算だけ、かなりみじめな出来と言えるのではないだろうか。
どうしたらいいのだろう。なに、どうにもしなくてよいのかもしれない。どうせこの先、大規模な筆算の割り算をする機会はそれほど大きくない。大学までゆけばこの手の計算は電卓でやって何の問題もないのであり、社会人となればなおさらである。漢字のトメハネや書き順と同じく、ふつうの会社で普通の仕事をしていて、割り算の筆算が問題になることなどないのだ。小学校中学校のほんの一時期に出会って使う、割り算の筆算がどのように面倒であろうと、よいではないか。
しかしそれではいかん。いかんのである。そんなものは「来年になったら自分が先輩になるのだから、部活の先輩の暴虐を我慢しなさい」というのと同じである。そういうことをやっているからいつまでも世界は平和にならないのであり、算数のかけ算に順序があるのだ。現にいま筆算をやっている、目の前の小学生をどうすればいいか考えようではないか。かれは割り算の筆算で四苦八苦していて、もう一回小学生をやっているつもりの私としては「将来筆算なんかしなくてもいいのだから今だけ我慢しなさい」とは言えない。消してやりなおし消してやりなおしではない、何かもっと頭のいい筆算アルゴリズムというものが、ないはずがない。なかったら考えるのだ。
というわけで考えてみた。こういうのはどうだろう。
いま、1076を128で割った商を、間違って7と推定してしまったとする。128×7は896なので、引いたら180である。しまった。商は7ではなかった。8だった。
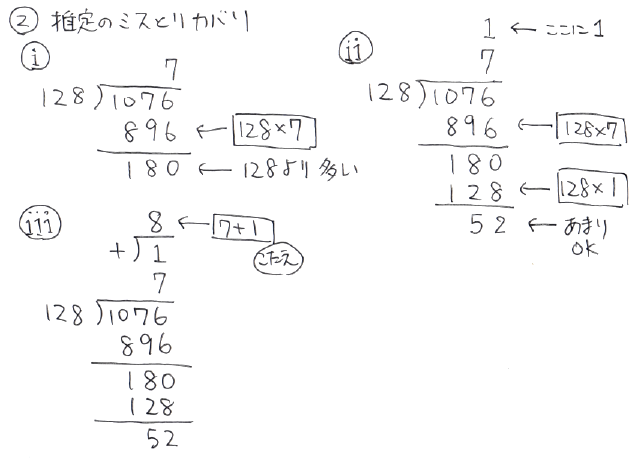
ここでやりなおさない。やりなおさないのである。消しゴムなどしまっておけ。そんなものはいいので、なるほどよくわかったあまりが180なのであれば、そこからもう一回128を引くのだ。さいわい、割り算の筆算というものは、引き算をしやすくできている。180引く128の答えは52。これがあまりである。商は7プラス1で8である。これでいいではないか。何がいけないのか。どうだろう。
この方法は、結局のところ、商の推定と、引き算を何回かに分けてやる、ということである。割り算の筆算は、何が難しいといって、商の推定なのだから、ここの負担を減らす。いいかげんでよいことにして、あとで修正が効くとかなり楽になる。計算が少し縦に長くなるとか、そういう難点はあるのだが、問題点を改良できた気がするのである。
さて、以上の方法は本当に有効なのか。「こんな方法を使わないで商の推定の精度をあげたほうがよい」という批判はあるかと思うし、だいいちこの方法には、減る手間(消してやり直す)がある一方、増える手間(複数回の掛け算、複数回の引き算、商の足し算)もあるわけで、どちらが本当に楽かは、おそらく場合によって異なる。どんな場合でも一律楽になる方法などない、気がする。さらにいえば、筆算はなにも学校の先生がその場で編み出したものではなくて、それなりの長い間、たくさんの人が関わって使ってきたものなのである。それを私ごときが数時間考えて改良できたりするものではない気がするではないか。それができる、と簡単に考えるのは、自分対世界、自分対歴史のスケール感を見失っていて、よいことではない。
そう思って、考えて、ちょっと私の子供達に話したまま、長いこと放っておいたのだが、先日、娘(中学三年生)の勉強を見ていたら、彼女がこのやりかたで割り算の筆算をやっていたので、驚いた。誰も見向きもしない、かえって面倒なやりかたはいくらでもある。教わったときは良さそうでも、実はそうでもない「改良」もたくさんある。ただ、ここに一人、これで楽になったと言ってくれる実践者がいるのだから、もしかしたらこれは長年使われてきたやりかたへの、何かの改良と言えるのかもしれない。そう思ってここに記録しておくしだいです。
※1 ここでどうしても、少し工夫して「過剰だった場合の修正方法もあわせて検討したらなおよいのではないか」と考えるものである。確かにそうで、このあたり、すこし考えてみたのだが、あまり踏み込まないほうがよい、などという結論に達した。まず、ぴったり正しい推定をする現状の方法と異なり、「これでは少ないかな」と保守的に見積もるだけで、すでにかなり楽になるもので、そこから先の改良は、比較的わずかしか手間を改善しなさそうである。どうもこういう「既存の計算を改良した」と称するものは、(上記のアイデアを含め)細々したルールが覚えづらかったりして、かえって面倒になる場合が多い気がする。あまり欲を出さないほうがよいかもしれない。
※2 さらに余談だが、割り算の筆算ではもうひとつ問題がある。19×8のような、(複数桁)×(一桁)の掛け算を暗算でやらないといけないところがそれで、大きな数の繰り上がりが出たりして、けっこうめんどうで、間違いやすい。これは、割り算とはそういうものなので、かなりしかたがない部分ではあるのだが、上の基本アイデアを使って、ここをもう少し楽にする方法があるかもしれない。
たとえば、誰でも考えると思うが「すでに計算した掛け算を使う」という方法がある。たとえば10618÷19などという計算のどこかで、すでに「19×5」を計算していたとすると、その計算結果を、あとの桁の計算をするときに使い回す。推定値は明らかに5よりも上だとしても、もう一回、とにかく既存の19×5を引いてしまう。そのあとで、小さくなった目標値に向けて小さな数の掛け算をやるのであれば、楽だし、間違えにくい。
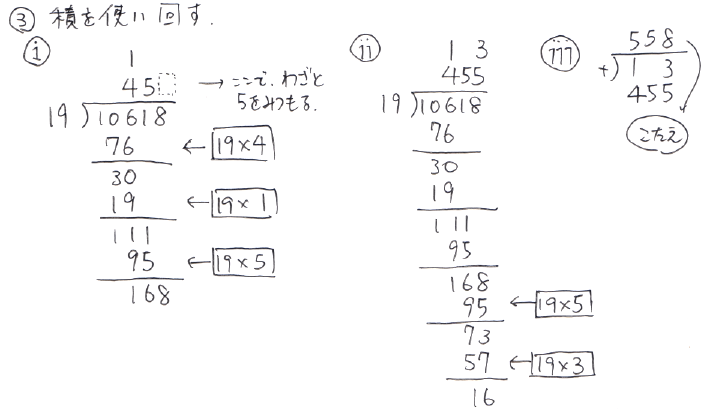
もう一つ、だんだん趣味的な改造になってきて、これでどの程度楽になるかどうかはわからないが、開き直ってしまえば「5以上ならとにかく5でいったん計算する」としてしまってもよいかもしれない。5を掛ける計算は、間違えにくいし、ゼロをつけて2で割って求めることもできて、確認も容易である。先に5を掛けた答えを欄外に書いておくなどして、それより上か下かをまず見て、上ならとにかく5を立ててしまう、などとしてもよいかもしれない。非常に自堕落なようだが、ここまでやると、6から9を掛ける、繰り上がり数が大きくなって面倒な計算をしなくてよくなるし、驚くべきことに、6から9の段の九九を使わなくて済んでしまうのである。
